
A Do not smooth time series, you hockey puck! Used to be scientists liked their data to be data. No more, not when you can change that data into something which is more desirable than reality, via the ever-useful trick of smoothing. Link.
B Do not calculate correlations (or anything else) after smoothing data. No, seriously: don’t. Take any two sets of data, run a classical correlation. Then smooth both series and re-run the correlation. It will increase (in absolute value). It’s magic! Link.
C Especially don’t calculate model performance on smoothed data. This is like drinking. It’s bound to make your model look better than she is. Link.
D Time series (serieses?) aren’t easy. Let’s put things back in observational, and not model-plus-parameter, terms. Hard to believe, but nobody, not even the more earnest and caring, have ever seen or experienced a model or its parameters. Yet people do experience and see actual data. So why not talk about that? Link.
E A hint about measurement error and temperature (time series) using the BEST results. Link. Here’s another anticipating that data. Link. Here’s a third using the language of predictive inference. Link.
F You’ve heard about the homogenization of temperature series. Now read all about it! A thick subject and difficult. This is the start to a five-part post. Link.
G Lots of ways to cheat using time series. Example using running means and “hurricanes.” Did he say running means? Isn’t that just another way of smoothing? Why, yes; yes, it is. Link.
H A “statistically significant increase” in temperature is scarcely exciting. One person’s “significant” increase is another’s “significant” decrease. Link.
I I can’t find a favorite, which shows the “edge” effect. If you use classical statistical measures, you are stuck with the data you have, meaning an arbitrary starting and ending point. However, just changing these a little bit, often even by one time point, can turn conclusions upside down. Michael Mann, “The First Gentleman of Climate Science” relies on this trick.
Here’s the précis on how to do it right, imagined for a univariate temperature series measured via proxy at one location.
A proxy (say O18/O16 ratio, tree rings, or whatever) is matched, via some parameterized model, to temperature in some sample where both series are known. Then a new proxy is measured where the temperature is unknown, then the range of the temperature is shown. Yes, the answer is never a single number, but a distribution.
This range must not be of the parameter, telling us the values it takes. But it must be the value of the temperature. In technical terms, the parameters are “integrated out.” The range of the temperature will always be larger than of the parameter, meaning, in real life, you will always be less certain. As is proper.
The mistakes at this level usually come in two ways: (1) stating the model point estimate and eschewing a range, (2) giving the uncertainty of the (unobservable) parameter estimate. Both mistakes produce over-certainty.
Mistake (1) is exacerbated by plotting the single point number. If the observable range were plotted (as noted above), it would be vastly harder to see if there were any patterns in the series. As is proper.
Mistake (2) plots the point estimate with plus-or-minus bars, but these (based on the parameter) are much too small.
Mistake (3) is to then do a “test”, such as “Is there a ‘statistically significant’ trend?” This means nothing because this assumes the model you have picked is perfect, which (I’m telling you) it isn’t. If you want to know if the temperature increased, just look. But don’t forget the answer depends on the starting and stopping points.
Mistake (4) is to ask whether there was a “statistically significant” change or increase. Again, this assumes a perfect model, perfect prescience. And again, if you want to know there was a change, just look!
Mistake (5) is putting a smoother over points as if the smoothed points were “real” and causative, somehow superior to the actual data. The data (with proper error bounds) is the data. This mistake ubiquitous in technical stock trading. If the model you put over your data was any good, it would be able to skillfully predict new data. Does it, hombre?
Everything said here goes for “global” averages, with bells on. The hubris of believing one can predict what the temperature will be (or was) to within a tenth of degree or what the sea-level will be (or was) within a tenth of millimeter fifty years hence is astonishing. I mean, you expect it from politicians. But from people who call themselves scientists? Boggles the mind.
Stay tuned for an example!
Is there actually any difference between “technical analysis” on market prices and numerology? I’ve looked for one but I can’t find it.
Pingback: (Most) Everything Wrong With Time Series | Skil...
Smoothing can be useful, even inevitable, in taking numerical derivatives of discrete data (a redundancy, I know) but one has to be very careful.
Briggs,
You NEED to get the book, Augustine’s Laws, by Norm Augustine (first written when he was CEO of Martin Marietta as I recall): http://www.amazon.com/Augustines-Chairman-Lockheed-Corporation-Augustine/dp/1563472406
He takes on project/program management, pretty much exclusively as managed by government contractors & their government overseers. His book highlights 52 such laws presented with whimsical graphs, on purpose, to make certain points.
The graphs & analyses are purposefully flawed to illustrate the right point — there’s real talent in accomplishing that. Using this book as a template & applying its tactics could really enhance the points you make.
Some of the graphs include:
– Actual program cost is directly proportional to the winning proposal’s thickness in millimeters. Illustrating that program development costs can be reduced via limits on bidder’s proposals.
– Required testing for simple things mandates nearly infinite tests while very complex systems (e.g. Peacekeeper missile) require hardly any testing at all (this required use of a log scale!). This illustrates that we can afford to develop & build very complex weapon systems but really ordinary things (e.g. artillery shells) will always be cost-prohibitive, at least relative to unit cost vs. technical complexity.
– Despite ever increasing program requirements for increasing system reliability, reliability has not improved. Shows: Government is very good & getting better at setting great goals.
– Hardware is NOT intimidated by rank (whereby it is shown that troubled programs moved under more senior-ranking top-managers did not do better). This illustrates a fallacy that appears in many disciplines (e.g., losing team’s performance is usually not turned around by firing & replacing the coach).
– Gross National Product (GNP) is directly proportional to lawyers (per capita). No surprises there, but the data backs this up….at least the data presented…
– The Classic: Trend data for the cost of each next-generation (the next technologically-based leap in capability) aircraft has increased logarithmically and extrapolation of this trend shows that in a very short time, many of our lifetimes, the US will only be able to afford one single next-generation aircraft, which the services will share during the week & the USMC gets to use on weekends. This trend has persisted quite accurately relative to projections–but the clever US Government has changed the presumed rules by getting allied governments to partner if they bring cash to the game: The Joint Strike Fighter (JSF). Who would’ve seen that coming – -maintain technological superiority by sharing the technology with close friends?
Each chapter is preceded by a segment of a sub-story, a mildly (only mildly) sarcastic story about how Daedalus model [toy] aircraft company competed for and won a government contract for the new [real] stealth airplane and then achieved success & riches by failing to deliver. This story, suitable for The Onion, but is painfully close to the truth.
Good sarcasm woven with accurate analyses, using intentionally flawed representations of accurately presented data, gets read, makes the right point, and has staying power (passes the test of time). Augustine’s Laws is reference that did it right. Not that anybody actually changed how they go about what they’re doing….
It is amazing how many good scientists:
1. Routinely miss or ignore autocorrelations in time series data, often leading to a significant overestimate of the number of degrees of freedom, and overly narrow uncertainty bands. It can also produce an error in the most likely trend, thought hat is usually small.
2. Fall for the smoothing siren. Alas they beckon scientific sailors who dash themselves on the rocks as they pursue smooth sailing (sorry)
H/t to Briggs for this post.
Why is that you think that data filtering is not desirable? It is true that defining noise isn’t always obvious. To somebody searching for undersea oil, a submarine is anoise while to the military the same submarine is a signal (as Morlet points out!). But once the problem in hand is defined (yes that is sometimes not very easy) droping out some information (the one coming for a source different than the one we are interested in) can be very useful (see for example image denoising technology – that is smoothing!). Furthermore what is the point of constantly processing massive amounts of information when the reality can be well (or sometimes better) described by much smaller subgroups of data (see mp3/mpeg/jpg files!)?
Ken – Augustine’s Laws was required reading at the Defense Systems Management College while I attended the PM course there. Its lessons were quickly ignored under the press of bureaucracy and politics.
Matt – Well said indeed: “the data (with proper error bounds) is the data.” When I view one of these multidimensional statistical grand scale presentations, I am often prone to ask – tell me about your outliers; explain why they are occurring. I rarely get a satisfactory explanation.
I also highly recommend Augustine’s Laws because I am living it. And let’s not forget C. Northcote Parkinson and his laws. Somebody needs to reteach these to the biz school professors.
Mr Kernel (inside joke),
Excellent question. Yes, sure, and absolutely, time series can be “smoothed”, i.e. have a model fit to them, especially when, as in noisy images, one suspects a “signal” is there but masked. But that’s because these models work for these data. I mean, there is a definite way to check that the model works.
This isn’t quite the case with, say, temperature. People experience the actual measurement, not a signal “underneath.” The articles linked explain this in more depth, but a smoother is only useful if it can be used as a skillful model to predict new data (never-yet-seen-in-any-way data).
Sure you need a model (some background assumptions) to extract a signal out of noisy observations. But lets not dig into an epistemological discussion (at least not yet). Filtering is not only used to extract signal. It is also used to study the frequency or multiscale attibutes of the series. We know that most time series can be expressed a sum of amplitude modulated sine waves with uncorrelated coefficients (alternative orthogonal representations are admissible too – see non-decimated wavelet representation). Filtering allows you to study the series at particular frequency ranges or scales. It is surely up to the researcher (or up to his model) to decide which frequencies/scales are the most relevant to the problem in hand. And I agreee that careless application of filtering may lead to spurious results (see for example http://epanechnikov.wordpress.com/2011/02/13/why-is-the-hodrick-prescott-filter-often-inappropriate/). However that does not mean that filtering , when used efficiently, is not a very valuable time series tool or that you should *never* smooth the series (i.e. use a wide bandwidth) when the data are not observed with error.
Epanechnikov,
I think Briggs is simplifying for the non-specialist. There are circumstances where you can validly calculate things, including correlations, from smoothed data, but the smoothing changes the statistical properties of the processing which can easily fool people who don’t know exactly what they’re doing. It’s a bit telling people not to mess with high-voltage power lines. The guys at the power company who maintain the lines know they can ignore it.
Just for fun, I decided to test Briggs’ claim that: “Take any two sets of data, run a classical correlation. Then smooth both series and re-run the correlation. It will increase (in absolute value). It’s magic!”
Here’s the R script I came up with. What do you think?
# ############################################
# Test claim smoothing increases correlation #
# ########################################## #
testsmooth = function(w) {
require(car)
# Generate some data – r is random noise, x and y have added rising/falling trends
r = rnorm(100)
x = r + w*(1:100)
y = r – w*(1:100)
# Apply Binomial smoothing kernel
bkern = c(1,4,6,4,1)/16
sx = convolve(x,bkern,type=”f”)
sy = convolve(y,bkern,type=”f”)
# Split chart area 2×2
par(mfrow=c(2,2))
# Top left
plot(x,main=”Rising data and smooth”)
par(new=T)
plot(sx,type=”l”,col=”red”)
# Top right
plot(y,main=”Falling data and smooth”)
par(new=T)
plot(sy,type=”l”,col=”red”)
# Bottom left
plot(x,y,main=”Scatterplot unsmoothed correlation”)
ellipse(c(mean(x),mean(y)), cov(cbind(x,y)), sqrt(qchisq(.95,2)))
# bottom right
plot(sx,sy,main=”Scatterplot smoothed correlation”)
ellipse(c(mean(sx),mean(sy)), cov(cbind(sx,sy)), sqrt(qchisq(.95,2)))
# Calculate and return correlations between unsmoother and smoothed data
cat(“Unsmoothed correlation = “,cor(x,y),
“\n Smoothed correlation = “,cor(sx,sy),”\n”)
}
testsmooth(0.02)
Eppy, NIV,
Here’s something even easier:
ni = 100
d = 0
for (i in 1:ni){
# fancy schmancy time series
T1 = as.numeric(arima.sim(n = ni, list(ar = c(0.8897, -0.4858), ma = c(-0.2279, 0.2488)),rand.gen = function(n, …) sqrt(2) * rt(n, df = 5))+70)
T2 = as.numeric(arima.sim(n = ni, list(ar = c(0.8897, -0.4858), ma = c(-0.2279, 0.2488)),rand.gen = function(n, …) sqrt(2) * rt(n, df = 5))+70)
# plain-Jane noise
#T1 = rnorm(ni)
#T2 = rnorm(ni)
a=cor(T1,T2)
# fancy schmancy smoother
b=cor(loess.smooth(1:ni,T1)$y,loess.smooth(1:ni,T2)$y)
# manly smoother
#b=cor(filter(T1, rep(1,5)), filter(T2, rep(1,5)),use=”pairwise.complete.obs”)
d[i] = abs(b-a)
}
hist(d,20) # 20 bars
plot(sort(d)) # for even more fun!
Use either the fancy-schmancy time series or the plain-Jane noise (you have to uncomment or comment out the relevant T1,T2). Then use either the fancy-schmancy loess smoother or the manly running means (same thing with comments). Lo! Increased correlations. (You can also take off the abs() on d).
Of course, any individual simulation may show a decrease, but most don’t.
The smoothing assumes a model, which as I said last time, is surely okay as long as it’s the right one. Where’s the evidence it is right? Well, in smoothing fuzzy pictures and the like, we can check. But, say, global average temperature?
Mr. Briggs,
SO A is WRONG, Mr. Briggs.
Of course, any individual simulation may show a decrease, but most don’t.
SO it is not magic, it B is S WRONG, Mr. Briggs!
I believe I have offered you a counter example in a previous post in which you made claim B.
(Resubmit… so I can be among the top 3 commentors. ^_^)
SO A is WRONG, Mr. Briggs.
Of course, any individual simulation may show a decrease, but most don’t.
SO it is not magic, B is simply WRONG, Mr. Briggs!
I believe I have offered you a counter example in a previous post in which you made the claim B.
Nullius in Verba,
Good thinking! The fact that x series has a positive slope (warming trend) and y series negative slope is important. Thinking theoretically, smoothing would increase the effect of the slopes and decrease the one of the common error r when calculating the correlation between smoothed( r – w *time) and smoothed( r+w*time). So, with a larger w, the correlation can also become negative after smoothing.
Mr. Briggs,
T1 = as.numeric(arima.sim(n = ni, list(ar = c(0.8897, -0.4858), ma = c(-0.2279, 0.2488)),rand.gen = function(n, …) sqrt(2) * rt(n, df = 5))+70)
I love those magic three dots, but R doesn’t.
JH,
No, A is right, for all the many, many reasons I outlined in the post. And so too is B right. I and NIV have offered actual working examples which show B is correct.
Of course, it’s always possible to find one series somewhere where correlation becomes smaller in absolute value after smoothing, but that means nothing. Aberrations abound. The general theory I offered in the original post is correct.
Here it is in brief. Take two time series and let them be smoothed. The more they are smoothed, the closer to straight lines they become. Any two straight lines are (linerally) correlated perfectly, i.e. the correlation equals 1 in absolute value. This is mathematical truth.
Of course, you have the degenerate cases where the smoothing brings one of both of the series to all 0, but that is nothing.
JH,
Well, I don’t have time to teach R to you, but probably what happened is that your browser turned those three dots into one character. You’ll have to change them to three to get it to work. This is R’s way of indicating many values may be passed to a function.
“And so too is B right. I and NIV have offered actual working examples which show B is correct.”
Did you run it?
“Here it is in brief. Take two time series and let them be smoothed. The more they are smoothed, the closer to straight lines they become. Any two straight lines are (linerally) correlated perfectly, i.e. the correlation equals 1 in absolute value. This is mathematical truth.”
I thought it might be something like that… 🙂
If you split the two signals into frequency components, you can think of the overall correlation being a combination of the correlation of the high-frequency components, added to the correlation of the low-frequency components, both weighted by how much variance there is at each frequency. This works out because the high frequency bits are not correlated with the low frequency bits: The integral of Sin(at)Sin(bt) is zero when a is not equal to b.
(Note, I’m hand-waving like mad here. Don’t believe what I say…)
The correlation is basically measuring how “in-phase with each other” the frequency components are, and adding up. Smoothing attenuates the high frequencies in the data, leaving just the low-frequency bit. Smoothing throws away information at the high-frequencies, where you hope most of the noise is. The ultimate result is to throw away all but the zero-frequency component, which gives a *horizontal* line at the average value of the data. Note, constants are *not* correlated.
Unrelated signals have unrelated frequency components, and the “in-phase-ness” at any given frequency varies randomly. As you average a broader band of frequencies, these random values average out to zero. But if you pick a narrower band, you get a smaller ‘sample size’, and a ‘noisier’ result.
Reducing the bandwidth of the data has much the same effect as reducing the length of the data, the sample size, but it fools people because the number of points is the same. If you imagined taking two unrelated series, and shortening them both by chopping points off the end, it wouldn’t be surprising to see the correlation starting to swing around more wildly. When you get down to the last two points, you’ll almost certainly get either perfect correlation or perfect anti-correlation – but it’s almost entirely down to the noise which you’ll get.
However, you can also play other games with it. The above is a consequence of the series being unrelated – it’s not true for series that *are* related in special ways. One thing you can do is to pick two series that are strongly correlated in their high-frequency components but anti-correlated in their low-frequency components. For example, take the same random series, but add opposing trends to them. (What I did in my R code.) Then when you look at the overall series you get positive correlation, but as you attenuate the high frequencies by smoothing, the anti-correlated low frequencies become more dominant. There is an intermediate point where they balance. (Somewhere around 0.02 in my R example.)
The result is a pair of series that have a strong positive correlation, but which when smoothed the correlation disappears. That’s because all the positive correlation is concentrated at the high frequencies, which smoothing throws away. It’s the same as if you designed a time series where the series started out of phase and gradually drifted into phase over time, and then you started shortening the data from the end. Instead of sample correlations getting bigger as the sample size reduced, they’d get smaller.
In summary, Briggs’ claim works for data that is actually uncorrelated, or mostly so, and also for data where most of the strong signal-based correlation (+ve or -ve) is concentrated at low frequencies, with mainly noise at high frequency. And it re-emphasizes his primary point: that smoothing gives counter-intuitive results that you have to do a lot of very fancy ‘advanced stuff’ to interpret correctly. Which of course non-specialists like climate scientists often don’t know about.
Don’t mess with the high-voltage power lines!
Mr. Briggs,
Let me repeat NIV’s response! Did you run it?
To show A and B are incorrect, one simply has to provide a counter example. NIV has provided you an example. No fancy-schmancy time series or R codes needed. A and B cannot be seen as two pieces of opinions. They are wrong. There are no polite ways to say they are wrong.
This is not what your claim B is. You are just making more and more incorrect claims.
A wider bandwidth results in a smoother curve, and the curve doesn’t have to be a straight line.
No, two straight lines are not correlated perfectly. A simulation of two lines in R will tell that you this is wrong. Two variables with perfect linear relationship indeed have a Pearson correlation of 1 in absolute value.
It’s okay to do it, JH. Just say “I guess I was wrong” and see how much better you feel.
Except for the degenerate case (slope of 0), two straight lines are perfectly correlated. Only a by-the-book frequentist would run a “simulation” to prove this. Why in the world would you need to “simulate” a straight line? It’s a straight line!
All,
This was fun, and is now homework.
Take any two discrete straight lines, say
a + b (1:n)
c + d (1:n)
And then prove that using ordinary Pearson product-moment correlation coefficient, the correlation must be +/- 1. Nothing more than algebra is needed.
The only wrinkle, as said, was restriction that |b|,|d| >0. This avoids dividing by 0, i.e. slopes of 0.
“Except for the degenerate case (slope of 0), two straight lines are perfectly correlated.”
True. But the degenerate zero-slope case is precisely what unlimited smoothing approaches. (At least, for any finite, stationary process.)
“Only a by-the-book frequentist would run a “simulation†to prove this.”
The lines in the simulation weren’t straight. That’s why I plotted them out, instead of just reporting the correlation coefficients. The idea was to enable one to see what was happening.
The basic idea is that the series are strongly correlated at high frequencies and weakly anti-correlated at low frequencies. Smoothing attenuates high frequencies, reducing the correlation. There is still plenty of wiggle at both high and low frequencies – the line is far from straight – but the positive and negative correlations of these wiggles cancel out.
The point is that the correlation increasing on smoothing is a *special case*, that applies over a wide range of the most common physical situations, but it is not a mathematical universal.
But I’d like to emphasise, this nit-picking doesn’t detract from the correctness of your *main* point, which is that smoothing changes the statistical properties of operations like correlation in unexpected ways: one cannot carelessly smooth-and-calculate and just hope all the messy stuff going on in the background will work out.
NIV,
Hmm. All soothing eventually degenerates to slope 0? I think you’re right and I’m wrong. If so, then it’s intermediate levels of smoothing, the types used in applications, which increase in correlation because the first step to degeneracy (slope 0) is a non-slope 0.
Update I’m still not convinced because as the smoothing increases and the series approach slope 0, the correlation involves a ratio, and therefore a limit is needed. Is the limit degenerate? I don’t know. But think of this: as the two series are almost but not slope 0, i.e. the series are nearly straight lines slopes almost but not 0, then the correlation still approaches +/- 1. It is only at the limit where there are difficulties. And that means we have to say how we got to the limit, how it is approached (this comment not for NIV, but for others not used to working with limits). So I can see how some smoothers could break down but I can imagine (no proof) that others might not.
But I agree (or still stand by) point that one cannot smooth at all when using the series for purposes skin to correlation.
Oh, the simulation comment applied to JH who mentioned she was simulating straight lines. Point was two (non-degenerate) lines are always perfectly correlated.
Nice codes and conversation.
William
“The smoothing assumes a model”
Yes indeed. A model or some moment assumptions. And yes there is sometimes no way to check whether some of these assumptions are right but then we might have some reasons to believe that some assumptions are more credible than others. All models (as gross simplifications of the reality) are furthermore wrong. Some are however useful. We don’t necessarily have to use the right model (which does not exist) to get a useful result.
” Well, in smoothing fuzzy pictures and the like, we can check.”
What we can check is whether the final result satisfies us aesthetically. Not whether it corresponds to the reality. Some of the “noise” you may have decided to remove might be masqueraded dust, snow or freckles. And then it all depends on what your define as signal and what as noise (which involves a decision wrt model/assumptions).
“I’m still not convinced because as the smoothing increases and the series approach slope 0, the correlation involves a ratio”
That is a special case which definitely happens when using a simple MA filter on circular series.
I agree that the behavior in the limit is tricky. It’s like the similar situation when we reduce the sample size – with three points it can go either way, with two points you almost certainly get perfect correlation or anti-correlation (unless the last two points are exactly equal), but what happens when there’s only one point left??!
However, the limiting case was an incidental note. I was primarily talking about the situation far from the limit, with intermediate levels of smoothing.
The R code generates concrete examples of pairs of sequences where the correlation reduces on smoothing. I’ve just run it 20 times, and in every case the correlation between the smoothed series was smaller in absolute value than the unsmoothed. While I would agree that the construction is a bit contrived, it’s still a broad class that’s quite robust to variation.
The difference in our views here is, I think, quite minor, and I’d be happy to pass on it. I’m only pursuing it at all because I think it’s an intellectually interesting example, and worth understanding.
By the way, I just realized I messed up the scales on the chart plotting. Inserting the following lines in the relevant place should fix it.
—
plot(x,main=”Rising data and smooth”,xlim=c(0,100),ylim=range(x))
par(new=T)
plot(sx,type=”l”,col=”red”,xlim=c(0,100),ylim=range(x))
# Top right
plot(y,main=”Falling data and smooth”,xlim=c(0,100),ylim=range(y))
par(new=T)
plot(sy,type=”l”,col=”red”,xlim=c(0,100),ylim=range(y))
Mr. Briggs,
I am trying to ignore your useless comment. However, I don’t really feel any better. I feel disappointed, kinda like how I feel when I grade students’ homework.
An anecdotal evidence is not enough to support a claim. However, one simple case is enough to show that your claim that two straight lines two straight lines are perfectly correlated is blatantly WRONG.
set.seed(222); x1=rnorm(100); y1=0.5+ x1; x2=rnorm(100); y2=0.5-0.5*x2; cor(y1,y2)
I am going to ignore the useless first sentence.
The point is not to simulate a straight line; it is to show that “two straight lines are perfectly correlated†is WRONG.
JH,
y1 and y2 are not straight lines.
plot(y1,type=”l”)
Does that line look ‘straight’ to you? Or wiggly?
Nullius in Verba you’ve raised some very good points (which unfortunately apply only when assuming stationarity). Smoothing does not always increase correlations. It all depends on both where the cross-power of the processes is concentrated. Smoothing increases correlations when there is not significant cross-power in low frequencies and when the skeleton of the processes has linear form (and of course when the process is weakly stationary).
Now lets examine those assertions. According to Herglotz’ theorem (when assuming stationarity) correlation is just a weighted average of cycles at different frequencies. The weighting fnuction has the properties of a probability density function which means that its weights add up to 1. Say we can filter the process so that all cross-power at a certain high frequency range (note: an MA filter does not exactly do that) is removed. The new process will have all of its power distributed at lower frequencies and the cycles at those frequencies will be weighted heavier than those at the original unfiltered process (since the weights should still add up to one). Now whether the correlation will increase or not it all depends on whether the original average is higher or lower than the average of the filtered process. When there is significantly high cross-power at higher frequencies and low cross-power at low frequencies (for example when the sceleton of one process is a linear while the skeleton of the other has a certain non-linear form) smoothing will decrease correlation.
JH,
I am this close to calling you the Debbie Wasserman Schultz of statistics, but I won’t because you know how much I love you. NIV is on the money. What you have presented are not straight lines. Straight lines are straight. And by straight, I mean straight.
The proof (as in proof) that two straight lines (both with non-zero slopes) are perfectly (Pearson) correlated is quite easy. I know you can do it if you like.
Eppy,
I appreciate these (and NIV’s) comments; I take both your points. Thanks very much.
No, y1 and y2 are not linear in even-spaced time! They are linear in x1 and x2 respectively.
In fact, two variables would have a perfect linear relationship when they both are linear functions of the same variable, e.g,, in your case, even-space time period. since, by a simple algebra, the variable y1 would be a linear function of y2… just as I stated as before.
Anyway, does it make sense that two lines have a perfect linear relationship?
Anyway, does it make sense to say that two lines have a perfect linear relationship?
Listen, Debbie, or whoever you are. JH is going to be P.O.ed when she finds out you’ve been using her account. So cut it out.
Mr. Briggs,
Even a humble congress woman like me knows that unevenly-spaced time series y(x_i) measured at unequally spaced times (x_i) are common in many scientific areas. Aren’t paleoclimate time series often unevenly spaced in time? It’s best not to limit your thinking to an even-spaced time series.
Since A and B are not that important in the analysis of time series, I will advise JH to drop the case… even though you are an avid fan of Sarah Palin.
Debbie,
Even a non-humble internet commenter should know when to admit an error. Two straight lines with non-zero slop are perfectly (Pearson) correlated. Go on, you can do it: admit the truth. I dare you!
Mr. Briggs,
As JH stated twice that two variables with perfect linear relationship indeed have a Pearson correlation of 1 or -1. Take the two variables you gave as an example, with n=100,
y1 =a + b *t, and y2 =c + d * t, (1)
where t=(1:100), and b and d are not zero constants. The above implies that
y1 = (b/d) * y2 + a – (bc/d) .
That is, the variable y1 is a linear function of the variable y2 and therefore, depending on the sigh(b/d), the Pearson correlation between y1 and y2 is either 1 or -1.
Again, JH further stated that there would be a perfect linear relationship between y1 and y2 as long as they both are linear functions of the same variable, which doesn’t have to be t (time 1:100). It could be any x, say x = rnorm(100), since (1) still holds.
As you can see, I don’t need a PhD degree in statistics to understand why JH was saying.
Next, let’s turn to what it means to say two lines are perfectly linear. Though, imo, it doesn’t makes sense to compute the Pearson correlation coefficient between two lines. However, it seems JH went along and assumed that you meant a pair of n values of two variables that fall into any two lines. So, she generated two lines. Clearly, y1 is linear in x1 and y2 is linear in x2. Two straight lines. Yes, I can rescale x1 and x2 as unevenly-spaced times.
Here we go again. Thankfully, JH specified a seed number… that is, same y1 and y2 can be generated.
set.seed(222); x1=rnorm(100); y1=0.5+ x1; x2=rnorm(100); y2=0.5-0.5*x2; cor(y1,y2)
Now run:
matplot(cbind(x1,x2), cbind(y1,y2))
(Sorry, too busy being a congresswomen to construct a fancy plot, however, please feel free to connect the dots to make it looks like a time series plot.
So do you see two lines in the plot?
And NO, correlation between y1 and y2 is NOT 1 or -1.
Why would JH admit to a mistake that she has not committed?
BTW, JH told me that she sent you a counterexample to the claim that smoothing would increases correlation a long time ago. She is happy that you that you finally get her point!
Debbie,
Just like your namesake, you find it impossible to admit to error. Well, that’s politics. I forgive you. We can still be friends.
Mr. Briggs,
I would appreciate it if you can just show that you understand what I was saying!
Let do this step by step!
So did you run the matplot and see two lines?
JH, Debbie,
They are two ways to say you are wrong. First, correlation coefficients should be adjusted when observations and not equally spaced. Second, any two completely uncorrelated random samples can be expressed as perfect linear combinations of two other random samples (for example X = aΩ where Ω=1/a X and Y=1/βΨ with Ψ= βΥ, α,β != 0). That of course does not make them perfectly correlated. If that was the case then all pairs of datasets somebody could have imagined would have been perfectly correlated!
You are welcome Briggs. 😉
Mr. Briggs,
So did you run the matplot and see two lines?
First
Correlation between y1 and y2 should be adjusted? OK…
(1) Define the correlation between two lines for me first. Then you can show me that two straight lines are correlated perfectly!
(2)Show me that the correlation coefficient after adjustment is 1 or -1!!!
Second
Your example doesn’t show that “any two completely uncorrelated random samples can be expressed as perfect linear combinations of two other random samples. \Omega and \Phi are derived by multiply X and Y be some constants. That is, X and Y are not expressed as perfect linear combinations of TWO OTHER random samples.
Here is a random sample generated by
set.seed(23); x=rexp(10, .5); y=rnorm(10,0,1).
Now, express these two random samples as perfect linear combinations of TWO OTHER random samples. No, x and y are not completely uncorrelated, but pretty darn close, It’s nearly impossible to generate two completely uncorrelated random SAMPLES, though I have cooked up perfectly uncorrelated x and y in one of your post before.
So if Correlation(X,Y) = 0, then Correlation(\Omega, \Phi) is still zero. In fact, correlation(X,Y) = Correlation(\Omega, \Phi) which can be easily shown by the definition of Pearson correlation between two variables or samples.
Anyway, what is the point of this?
Handwavingly, to smooth a time series (not parametric curve fitting) into a straight line is basically taking the average of all data.
Also note that there are differences between “random variables†and “random samplesâ€. Just as the definitions of Pearson correlation and sample Pearson correlation are different. So I am assuming whatever is appropriate in my comment above.
α) The easiest way to calculate correlations on unevenly spaced data is first to transform them to evenly spaced data via interpolation. In your example we know the exact data generating models and hence it is dead easy to do so without introducing any bias at all (hence I won’t refer you to the relevant literature). See below:
set.seed(222); x=rnorm(200); y1=0.5+ x; y2=0.5-0.5*x; cor(y1,y2)
[1] -1
β) What I’ve meant is that all random variables are linear to infinite other random variables. The fact that X might be linear to Ω (where Ω= 1/αΧ) and Y might be linear to Ψ (where Ψ = 1/βΥ) does not imply anything about the correlation between X and Y. What you’ve done is that you’ve randomly chosen a number points on two lines and you’ve concluded that because those points are uncorrelated the lines are also uncorrelated. Sorry but that is extremely naive.
“No, x and y are not completely uncorrelated, but pretty darn close…”
Do you understand the concept of sample estimates? The concept of sampling error? You’ve generated a limited number of (artificial) observations from two known linear models and you’ve concluded that the variables are not completely uncorrelated since your sample estimate is not exactly equal to zero!
set.seed(222); y1=0.5+ rnorm(100); y2=0.5+rnorm(100); cor(y1,y2)
Obviously the same line is uncorrelated with itself since if we choose random points on exactly the same line those random points (surprise surprise) will be uncorrelated.
Now lets get a bit serious
Epanechnikov,
The above is not my codes! It’s yours. Yes, if you use the same x to obtain y1 and y2, then the correlation is -1. The above simulation boils down to what I said “two variables with perfect linear relationship indeed have a Pearson correlation coefficient of 1 in absolute valueâ€; see my previous explanations.
However, (somehow x2=rnorm(200) wasn’t copied into my previous comments,) please examine my codes below carefully and slowly.
set.seed(222); x1=rnorm(200); x2=rnorm(200); y1=0.5+ x1; y2=0.5-0.5*x2; cor(y1,y2)
Get rid of the word “might†and go through the definition of (sample) Pearson correlation coefficient between variables for (X,Y) and (Ω, Ψ), you will see I am correct. If you don’t want to show this by calculations, try simulations.
This is not what Briggs is talking about, is it?
Did you notice I capitalized the word SAMPLES? BTW, unless you want to count a constant model as a linear model, I didn’t not generate two linear models using the following codes:
set.seed(23); x=rexp(10, .5); y=rnorm(10,0,1).
No hypothesis testing at all. “No perfectly correlated” here means a non-zero correlation coefficient.
Just to be clear the following codes are written by you.
set.seed(222); y1=0.5+ rnorm(100); y2=0.5+rnorm(100); cor(y1,y2)
Oh, no, y1 and y2 generated by your codes are not the same line or more appropriately, they are not the same set of numbers. The computer will automatically update the seed every time it produces random numbers.
If y1 and y2 represents the same line, I mean, the exact same line, the correlation coefficient between y1 and y2 is 1. When a variable is correlated with itself, it will always have a correlation coefficient of 1. A well-known fact.
The reason that your codes result in a small value of correlation coefficient between y1 and y2 is that the rnorm(100) for y1 and the rnorm(100) for y2 are generated independently.
You know, I really don’t like grading. I always tell my students to get serious… because when everyone does the homework correctly, it saves me a great deal of time and frustration.
“The above is not my codes! It’s yours….. please examine my codes below carefully and slowly.”
I’ve mentioned the word interpolation
““No perfectly correlated†here means a non-zero correlation coefficient.”
All estimates (almost) always deviate from the TRUE value of the parameter they estimate. The question is whether the estimate is significantly different to a value which we might have reasons to believe is true.
“Just to be clear the following codes are written by you.”
Indeed
“y1 and y2 generated by your codes are not the same line ”
So you believe that two non identical lines may cross both y1 and y2. Euclid has a different opinion…
I anyway don’t think there is any need to continue this conversation.
Yes, Euclid would disagree with you on what you think I believe. It means that the100 data points {(rnorm(100), y1)} generated by your codes fall on a line and {(rnorm(100), y2)} fall on another line. Plot them.
No, I don’t see any point in continuing the conversation, either.
“Plot them. ”
set.seed(222); x1<- rnorm(100); x2<-rnorm(100); plot(x1,y1,col="4"); points(x2,y2); lines(c(x1,x2), c(y1,y2))
Over and out
(y1,y2 are of course defined as above: y1=0.5+ x1; y2=0.5+x2;)
(y1,y2 are of course defined as above: y1=0.5+ x1; y2=0.5+x2;)
yes, these two are the same line. Yes, you are correct. I thought wrong. (I kept thinking about my own codes.)
Ha… more to show that it doesn’t make sense to say that
“two lines” are perfectly correlated.
Hi Debbie!
Still denying two straight lines (with non-zero) slopes aren’t perfectly (Pearson) correlated? I bet you also were in favor of Obamacare.
Still haven’t done the proof, eh. Tell you what. Assign it to any of your first-year math-stat undergrad students. Should take them about 15 minutes, or less.
You can do it: repeat after yourself, “I was wrong.”
All,
This is for Debbie, who will, it is predicted, find a way to question the axioms of mathematics, or say “Oh, you meant straight lines”; anything to avoid admitting error.
Pearson correlation is defined (eventually) as:
(1)
and e.g.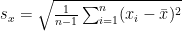 .
.
Two straight lines can be written as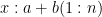 and
and 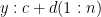 , where (1:n) are the discrete points where we measure the line. This needn’t be these consective numbers (we could start at, say, i=17) but they have to match for x and y, which they will because these are the points at which we measure the two lines (think of any ordinary x-y plot).
, where (1:n) are the discrete points where we measure the line. This needn’t be these consective numbers (we could start at, say, i=17) but they have to match for x and y, which they will because these are the points at which we measure the two lines (think of any ordinary x-y plot).
It helps to first figure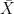 , which is
, which is 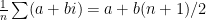 ; similarly for the mean of y. It is also obvious the (n-1)s cancel in (1). Now
; similarly for the mean of y. It is also obvious the (n-1)s cancel in (1). Now 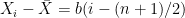 and
and  . So
. So 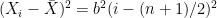 and similarly for y.
and similarly for y.
Then the numerator of (1) is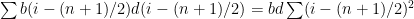 and the denominator in (1) is
and the denominator in (1) is 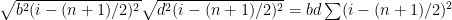 . We are left with
. We are left with
which equals either +1 if b and d have the same sign, or -1 if b and d have opposite signs. If b or d is 0 the problem is undefined.
Thus it is proved that two straight lines with non-zero slopes have perfect (Pearso) correlation.
Pingback: Somewhere else, part 88 | Freakonometrics
i have no training n statistical analysis but words have a meaning, to filter noise ..you must know it is noise.. filtering mean you separate one thing from another… the efficiency of even the validity of your filtering can be seen.. if you have a way to see that what remains is a meaningful signal…meaningful .suggest a goal a purpose whom success can be seen…