The plot atop this post is one of an observable, the cause of which is known to be related to a variety of physical, chemical, biological, geographical, and even sociological factors. The data is real, but I’ll disguise its source. All I can say is that it is measured out-of-doors. The points are yearly averages, from 1993 to 2014, of the same observable which itself is measured at hourly intervals (i.e. each point is the numerical mean of about 365 x 24 points; there is the odd missing value, and there are leap years).
It is obvious, I hope, that the values of (let us call it) X have changed. It is equally obvious that some thing or things caused X to change. In fact, since the points of X shown are averages of hourly measurements, there must be many (to say the least) causes of each point.
Thus far, this time series is like myriad others.
Now, it turns out that at some year a policy was changed such that some of the underlying physical, chemical, biological, geographical, and sociological were required to be changed. The human controllable parts, that is; this was a one-time change. The natural question, and a good question, is how much effect did the policy change have?
The answer is: nobody knows and we can’t tell with certainty, nor with anything like certainty. The short reason why we can’t know is because we don’t know the causes of X, therefore we don’t know how the policy changed all the causes of X, therefore we have no solid idea why X changed.
Reversing that, supposing we did know the causes of X, then we (of course) would know why X took each value, and we therefore would know how the causes change due to the policy, and therefore we would know the exact changes in X if the policy were in place or if were it not.
This much should be obvious. But there has developed a tradition in classical (mainly frequentist, but also Bayesian) statistics which purports to reveal the changes in X due to a change in policy. I don’t want to delve deeply into the statistical methods, since our purpose is philosophical. I’ll instead say it was asserted that because there was measured a “statistically significant” upward trend after the policy was implemented, that therefore the policy had worked.
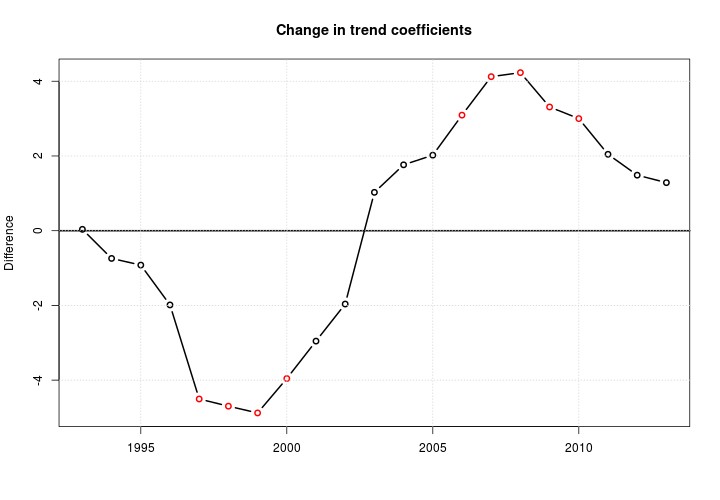
This cannot be so. Here is why. Here is a picture of the difference in trend coefficients from linear regressions, first regressing 1993 versus 1994-2014, then 1993-1994 versus 1995-2014, and so on, up to 1993-2013 versus 2014. The points are colored red if the p-value associated with the difference in trend coefficients is wee, else it is black if the p-value is not wee.
It isn’t quite the same, but if you have heard of “tests for differences in means” (always a misnomer), think of those. For example, the first test is for the mean of 1993 (which is just 1993) versus the mean of 1994-2014, and so on. The difference in means (or thereabouts) are the dots. Take 2000: the red dot says the mean (or thereabouts) of X from 1993-2000 was “significantly” lower than the mean of X from 2001-2014.
Now the mean of 1993-2001 was also lower than the mean from 2002-2014. It was not “significantly” lower. But was it lower? Yes, sir, it was. Some thing or things caused the differences in means in both cases. The interpretation of “significance” is one of two things, both of which are always (as in always) wrong.
(1) A classical statistician will say some real thing caused the change from 1993-2000 to 2001-2014, and he will also say “chance” or “randomness” caused the change from 1993-2001 to 2002-2014. Chance and randomness are not physical, they have no causal powers; therefore, they cannot cause anything. When this is pointed out, the statistician will then say that he does not know what caused the 1993-2001 to 2002-2014 shift. And that is fair enough, because typically he will not know. Yet here we do know there multitudinous causes which, we can infer, must have changed in magnitude between the two time periods. Where or when or how we cannot say.
Yet pause. The statistician is obliged to say some real thing caused the shift from 1993-2000 to 2001-2014. Now all we have in the “data” are years and values of X. It turn out that neither 2000 nor 2001 were the years of the policy change. Because the change is “significant”, the statistician must declare that some thing (or things) changed, but he doesn’t know what. But we have already agreed that some thing (or things) changed between the periods 1993-2001 and 2002-2014, even though these changes weren’t “significant”. What’s the difference between “significant” and not “significant”? Well, there isn’t and cannot be one: the concept is entirely ad hoc, as we see next.
(2) Since the statistician (nor you or I) does not know what causal changes took place between 1993-2000 to 2001-2014 and between 1993-2001 to 2002-2014, but he must say change did occur in the first place but not the second, because the first shift was “significant” but the second was not, he will say the parameter which represents change in the first shift really did change, but that the parameter which represents change in the second shift did not change and is in reality equal to 0. The parameter is the mathematical object in the regression that says how the central parameter of the normal distribution which represents uncertainty X changes when shifts occur. (Regression is about changes in parameters, not observables, unless they are turned into predictive models.)
Consider this carefully. The statistician will admit that a shift took place between 1993-2001 to 2002-2014, and he knows the shift must have been caused by some thing (or things), and he must admit this thing cannot be chance, because chance isn’t ontic, so he will say that the parameter did not change and must be set equal to 0. Now parameters are just as real as chance, so that physical events cannot operate on them. This means the parameters, and the models themselves, are purely a matter of epistemology; they only represent our uncertainty given certain assumptions. Nothing in nature could change the parameter, which calculations show is not equal to 0, so it is a pure act of will on the part of the statistician to set it equal to 0.
And this is fine: the statistician is free to do whatever he wants. The model can be made predictive assuming the parameter is 0 or non-zero. But in no way can the statistician assert that no changes in cause occurred, because of course they did. Causal changes also occurred between 1993-2000 to 2001-2014, and the statistician is free to accept the non-zero value of the parameter. In both cases, the statistician has no idea what happened to the causes, except that they changed.
Result? Probability models cannot ascertain cause, nor changes in cause. If causes were known, then probability models aren’t needed. Probability models cannot ascribe proportional cause, either. If we added terms to the regression, all the model would tell us is if the term changed in such-and-such a way, the uncertainty in X goes up or down or whatever.
To understand cause, we must look outside the data and try and understand the essence and powers of those factors related to X. Finding cause is brutal hard work.
(3) I’m not going to tell you when the policy took effect. But consider that the change-point test would typically only be done for this year. I went the extra step of pretending that the policy changed in 1994, then pretended it changed in 1995, and so on. This extra analysis shows you how over-confidence occurs. After all, look at all those “significant” shifts! As mentioned, the policy was a one-time thing. That means lots is happening here: and it would mean lots is happening even if there weren’t any red dots. If any change occurs, cause changes.
And even if no dot changed, cause still changed. How do we know? Because we know the policy must have done something, given our outside knowledge. But it could be that after it was implemented, counter-balancing causes took place and affected X such that X did not move. Call this the Doctrine of Unexpected Consequences (to coin a phrase).
No. To discover the effects of the policy, we must do the hard work of going every place the policy touched and doing the labor of measuring as many of the causes as possible.
(4) A note on predictive models. Every probability model should be examined in its predictive, and not parametric, form. We almost never, except in rare circumstances, care about the values of parameters. We care about the observables. What we want is to say, given a change in some variable, here is the change in the uncertainty of X. Everything is stated in terms of measurable observable. No statements about parameters are made. Testing is not spoken of. Terms are put in models because they can be measured or because decisions can be made about that, and that’s it.
Much, much, much more on this in Uncertainty: The Soul of Modeling, Probability & Statistics.
Notes: some might suspect correcting for “multiple testing” will fix this. It won’t. Make the p-values as wee as you want, the interpretation is the same. Some might say, “Why I’d never use that model! Everybody knows the Flasselblitz is the best model for this kind of data.” It makes no difference.

To discover the effects of the policy, we must do the hard work of going every place the policy touched and doing the labor of measuring as many of the causes as possible.
Well, presumed causes. After all that hard work, how does one identify the cause(s)? What will make these new measurements confess? Aren’t we still left with heaps of uncertainty?
@Gary, maybe and maybe not. Take a simple chemistry setup. Get a bomb calorimeter set up. Put a measured mass (derived from weight in Earth’s gravitational field) of carbon and oxygen in the calorimeter. There will be systematic and ‘random’ errors in the measurements plus scale resolution and accuracy of the scale. Apply a spark (heat). The chemical reaction starts. We can use a thermal expansion proxy to estimate the amount of energy released by the reaction.
So what do we know and what do we not know from this? Repeated often enough and carefully enough, we can get high resolution results from which we can predict an estimate of what your heating bills could be. We will not be able to tell you which atoms reacted.
Briggs says in regard to an observed change in a trend that correlates with some policy that was implemented:
“I’ll instead say it was asserted that because there was measured a “statistically significant” upward trend after the policy was implemented, that therefore the policy had worked.
“This cannot be so. Here is why.”
Following that comes some analysis, true enough, for what it’s worth (which isn’t much). Then comes this:
“To understand cause, we must look outside the data and try and understand the essence and powers of those factors related to X. FINDING CAUSE IS BRUTAL HARD WORK.” [emphasis in CAPITALS added]
The “brutal hard work” of finding causes ought to be the core message presented here (and by “causes” that means causes for things that happened, are happening, AND, will happen if something important isn’t changed).
All the philosophizing about models, their limits, and so forth — true they may be — are of very limited, negligible, or even counterproductive value if one lacks the means and know-how to do the “brutal hard work” of ferreting out causes. And their effects.
Take ENRON, the infamous company (one anyway) whose business plan, investor recommendations and so on & on, were supported by models. The evidence was there, long before the infamous downfall & bankruptcy, to see it (and other firms) were a financial “house of cards” whose doom was inevitable. Many people refused to believe the analysis-based-forecasts of the inevitable bankruptcy were true even as those “cards” were falling and Enron’s finances were crumbling.
All the statistical philosophical understanding will not help anyone recognize a similar situation (except in hindsight). One remains incapable of doing the BRUTAL HARD WORK of finding ’cause’ Briggs [finally!] touched on unless one is learned in the applicable “physics of the given situation.” Part of that “physics” is understanding that many people who ought to, and generally do, know better simply refuse to believe their own eyes.
Here’s a quote everybody should maintain if they’re involved in financial analysis, and is equally useful in most anything else as it cuts to the core of how dubious pretty much all data is, not to mention the models built on such data:
“They all have reputable audit firms. That’s one thing I want you to take away from this course: Every big fraud had a great audit firm behind it.”
– Jim Chanos, short seller & founder and president of Kynikos Associates, describing one common trait associated with every major corporate financial fraud, including but not limited to Enron, which he predicted well before it happened.
“And you know,” Chanos once mused to an interviewer, “there are ten thousand highly paid analysts and investment bankers and PR agents who are out shilling for corporations all day along and no one seems bothered by that.”
– Such may be the quality of financial data. The same dynamic holds true in many other arenas (climate data being the obvious one discussed here).
@cdquarles
We’re less interested in prediction of future observations than knowing the cause(s) of the past ones. With your simplified example, possible causes of the reaction aren’t many and therefore the predominant or only one can be deduced with little uncertainty. It’s the spark what did it (although there could be some other unknown cause). Taking Briggs’ example, which looks similar to plots of average global temperature from 1993-2014, even if we scrupulously measured the multitude of possible causes, how would we prove which one(s) were responsible?